etcd-io__etcd/pkg/adt/README.md

Red-Black Tree

"Introduction to Algorithms" (Cormen et al, 3rd ed.), Chapter 13

1. Every node is either red or black.
2. The root is black.
3. Every leaf (NIL) is black.
4. If a node is red, then both its children are black.
5. For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

For example,

import (
    "fmt"

    "go.etcd.io/etcd/pkg/adt"
)

func main() {
    ivt := adt.NewIntervalTree()
    ivt.Insert(NewInt64Interval(510, 511), 0)
    ivt.Insert(NewInt64Interval(82, 83), 0)
    ivt.Insert(NewInt64Interval(830, 831), 0)
    ...

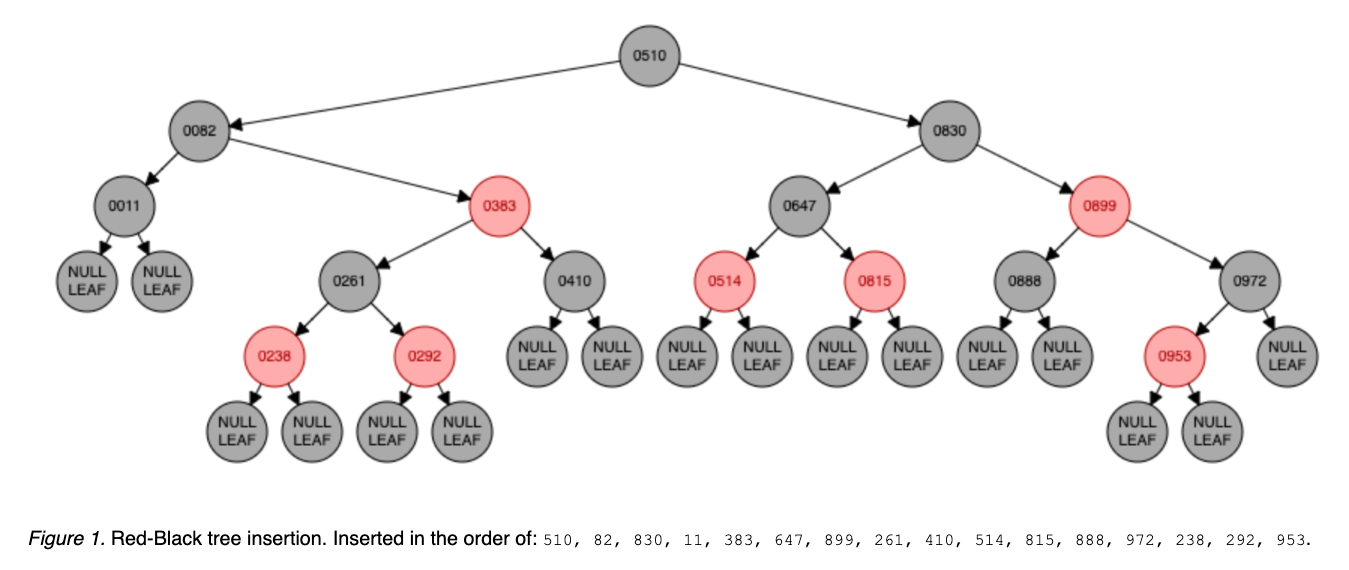
After inserting the values 510, 82, 830, 11, 383, 647, 899, 261, 410, 514, 815, 888, 972, 238, 292, 953.

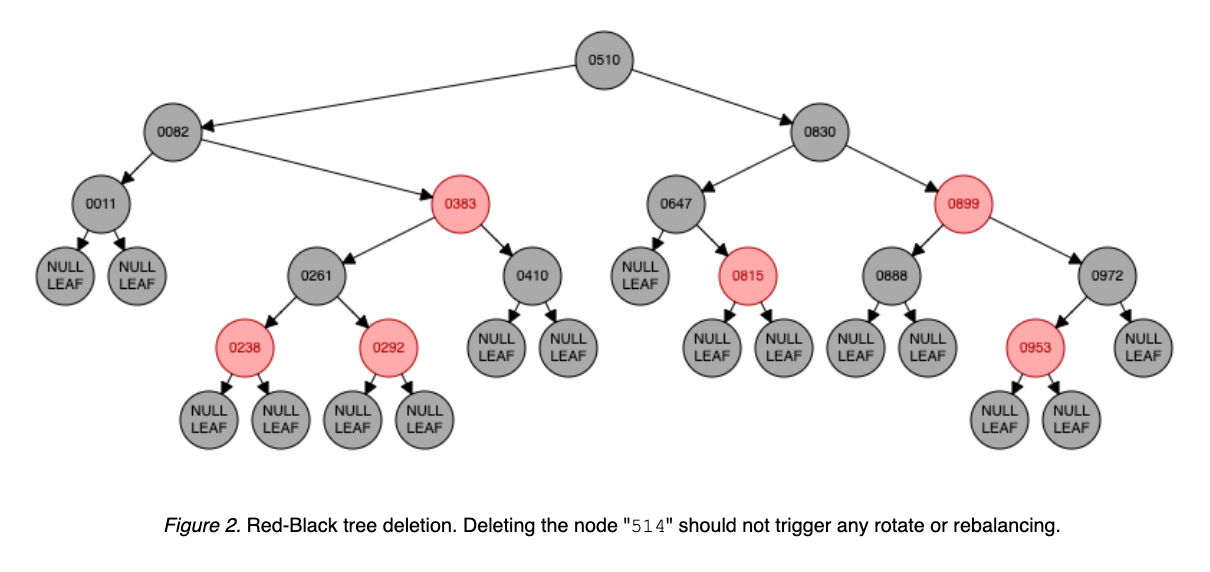
Deleting the node 514 should not trigger any rebalancing:

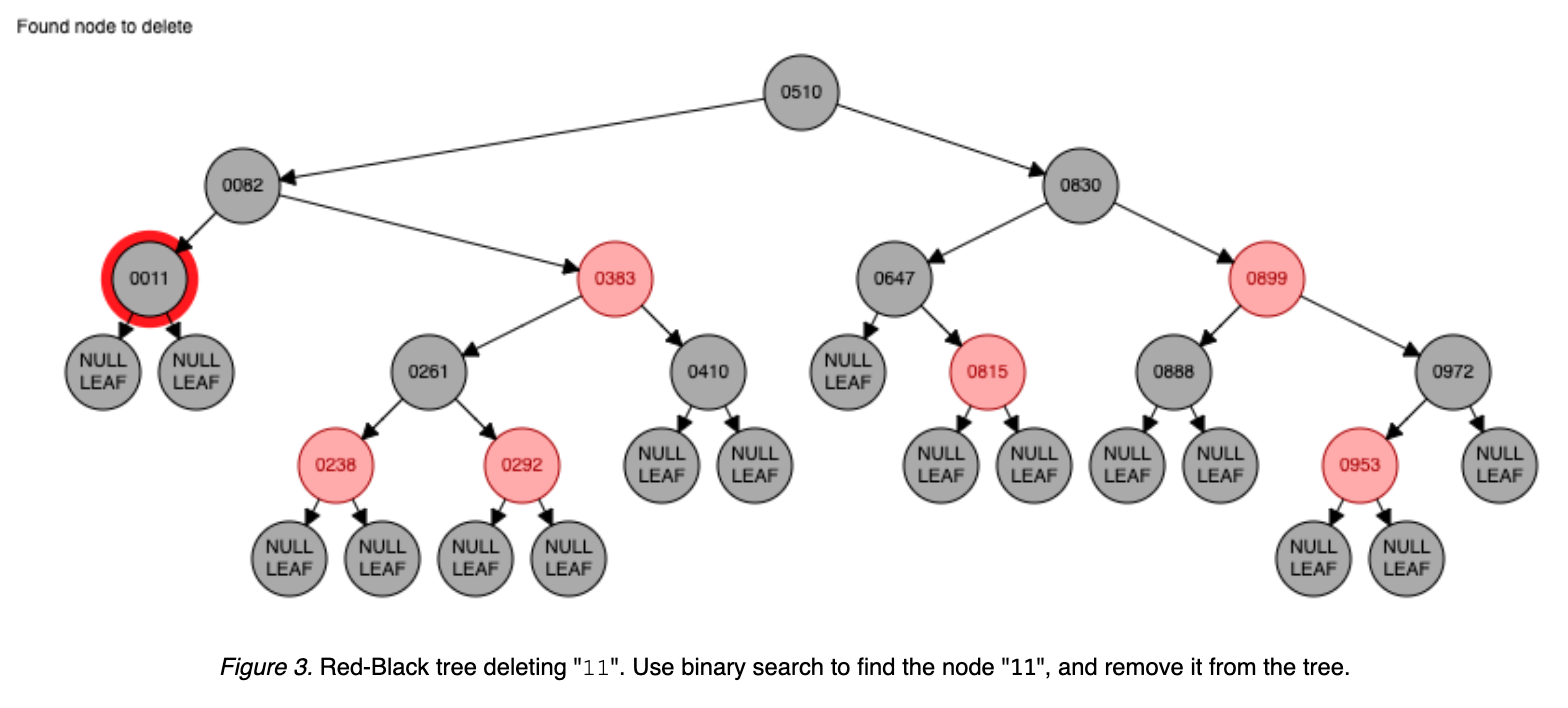
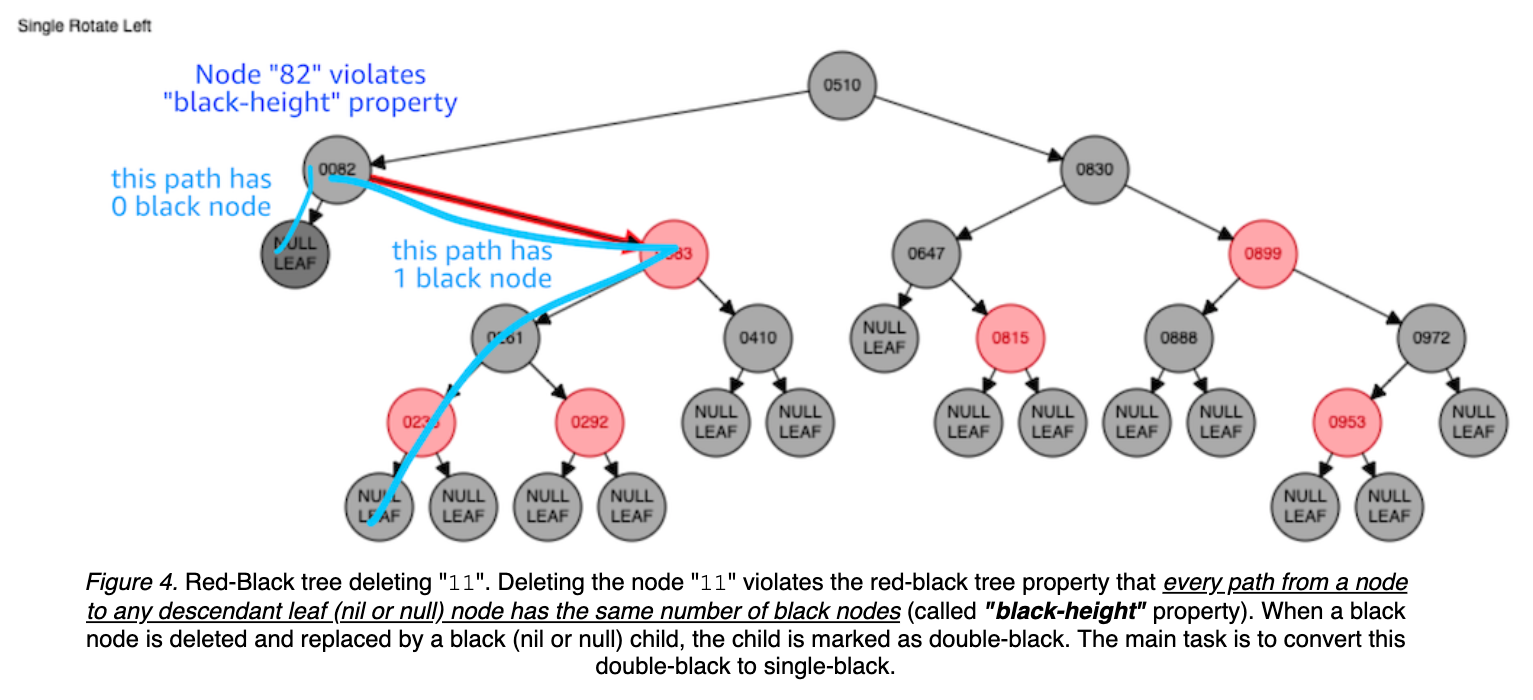
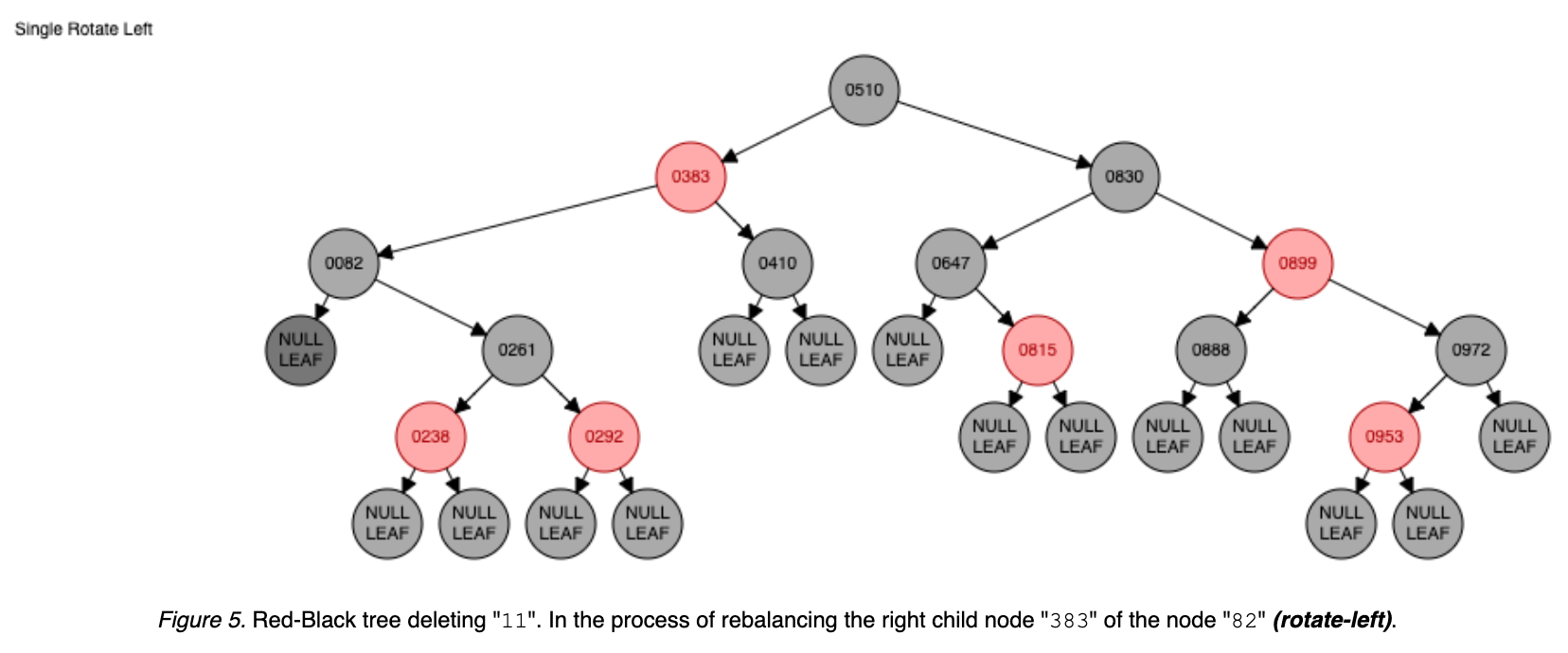
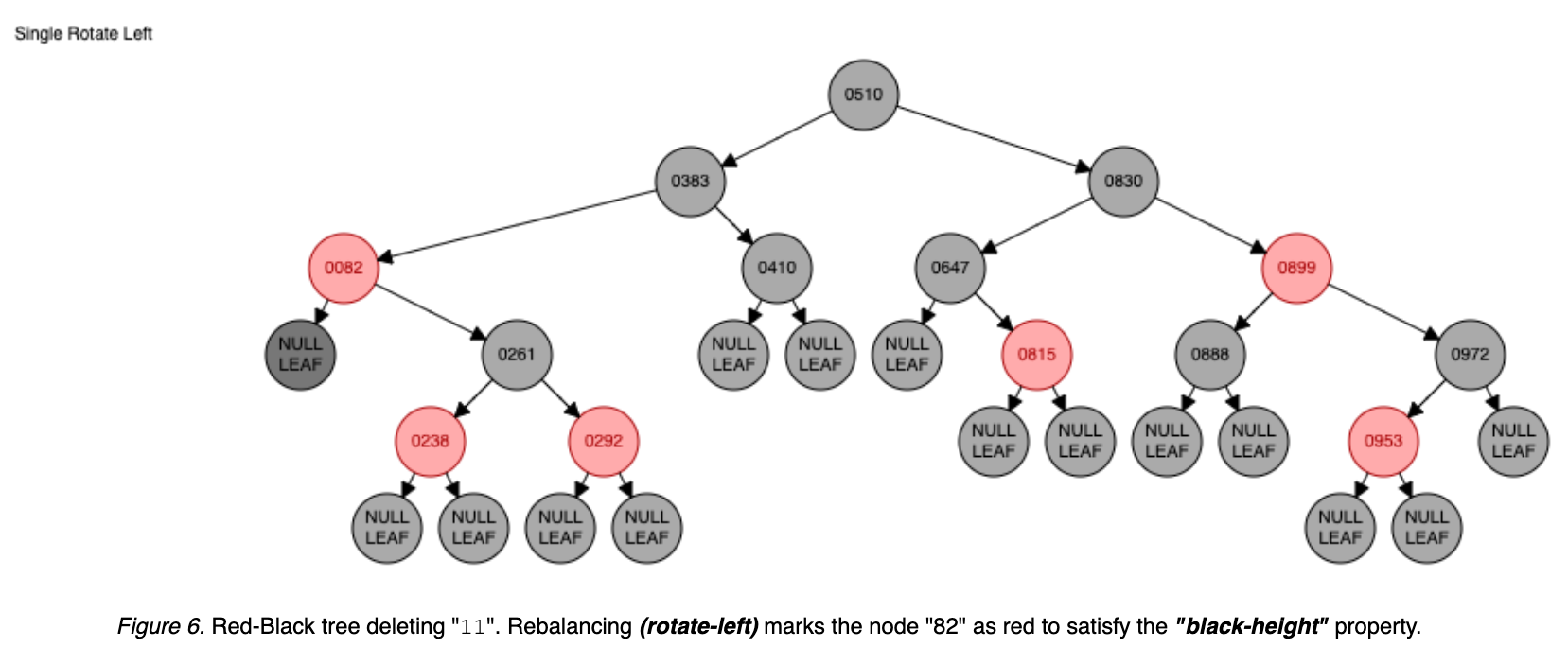
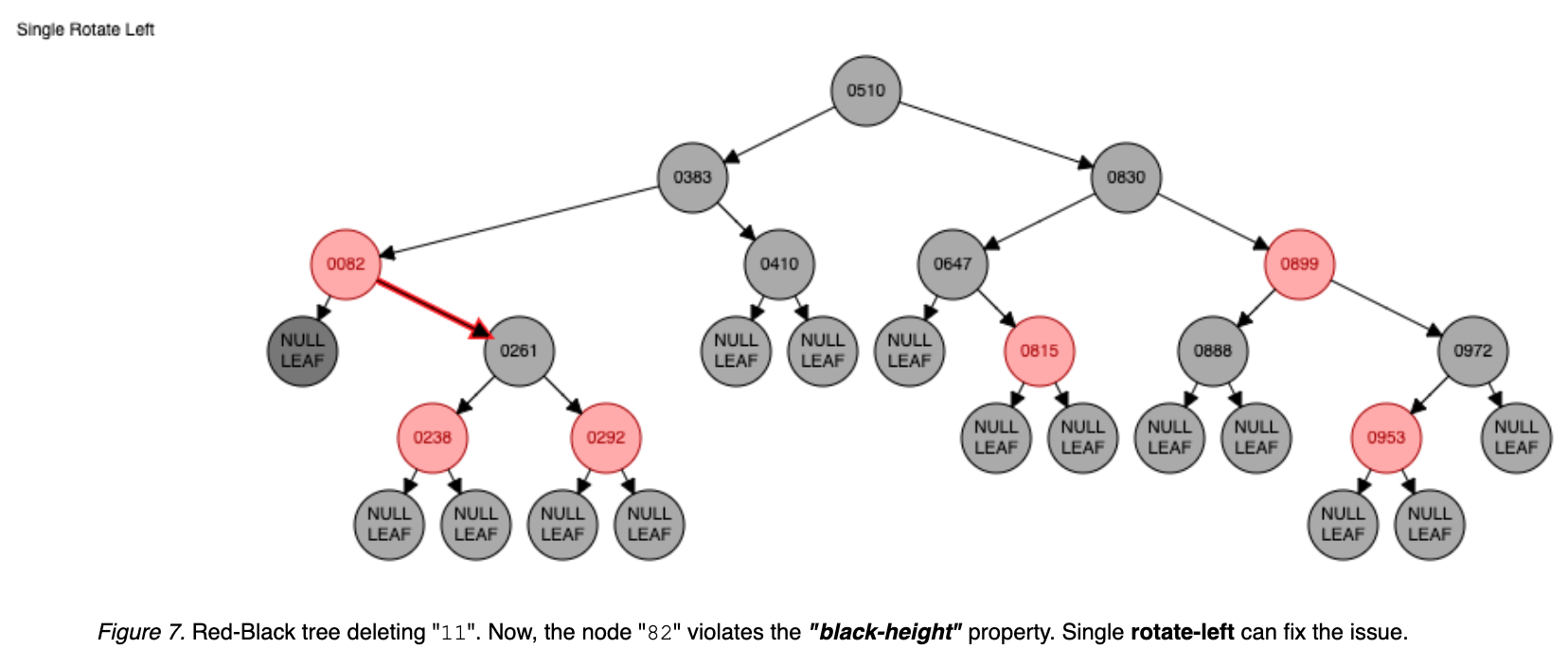
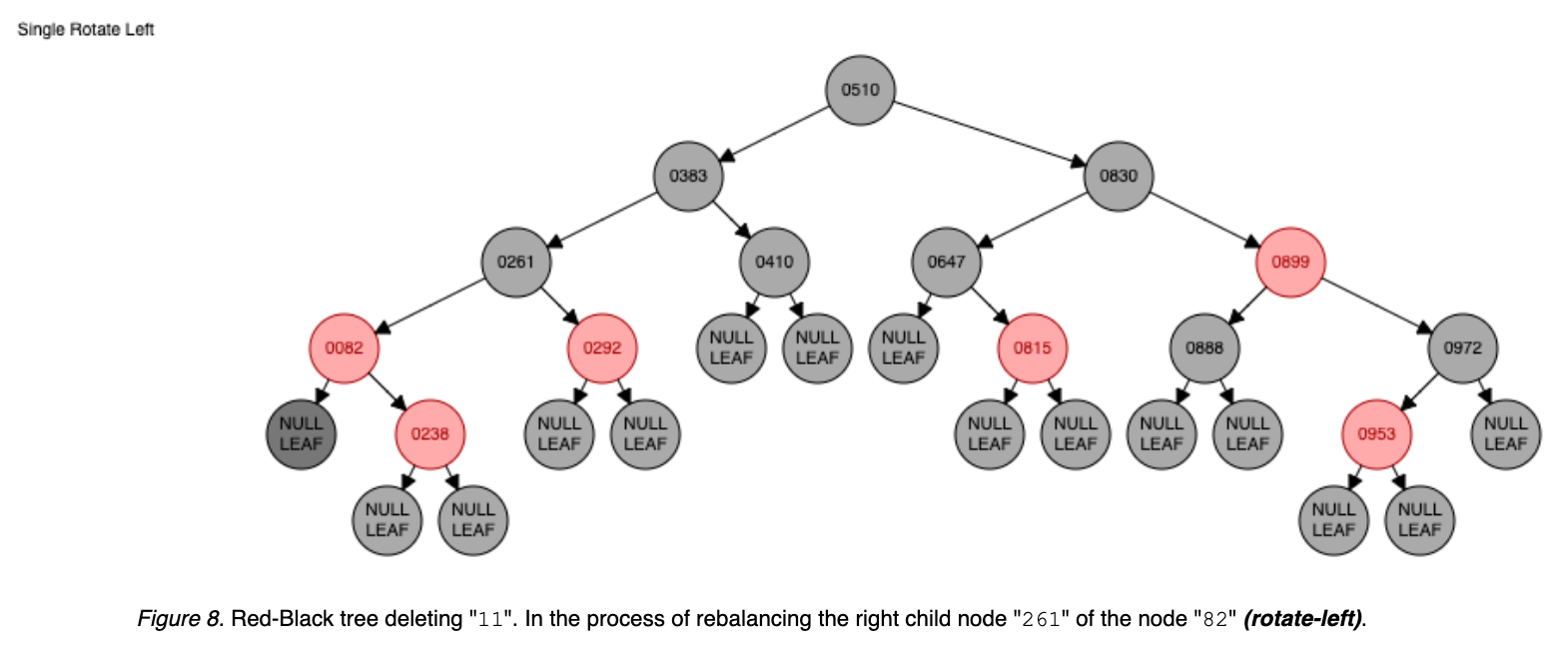
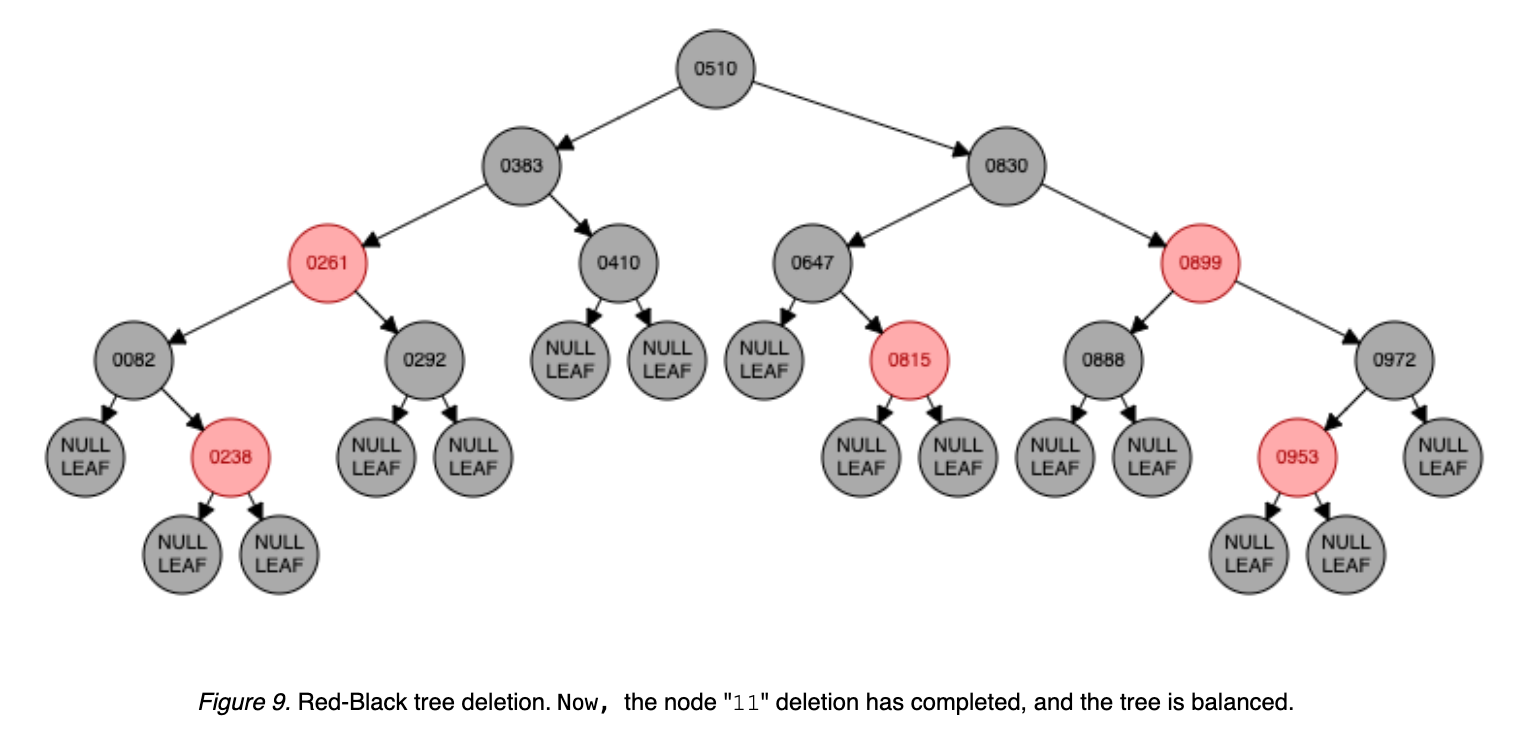
Deleting the node 11 triggers multiple rotates for rebalancing:

Try yourself at https://www.cs.usfca.edu/~galles/visualization/RedBlack.html.